3  How to choose an estimand: Real-world example

3.1 1. Extent to which the risk of OUD conferred by chronic pain operates through pain management treatments

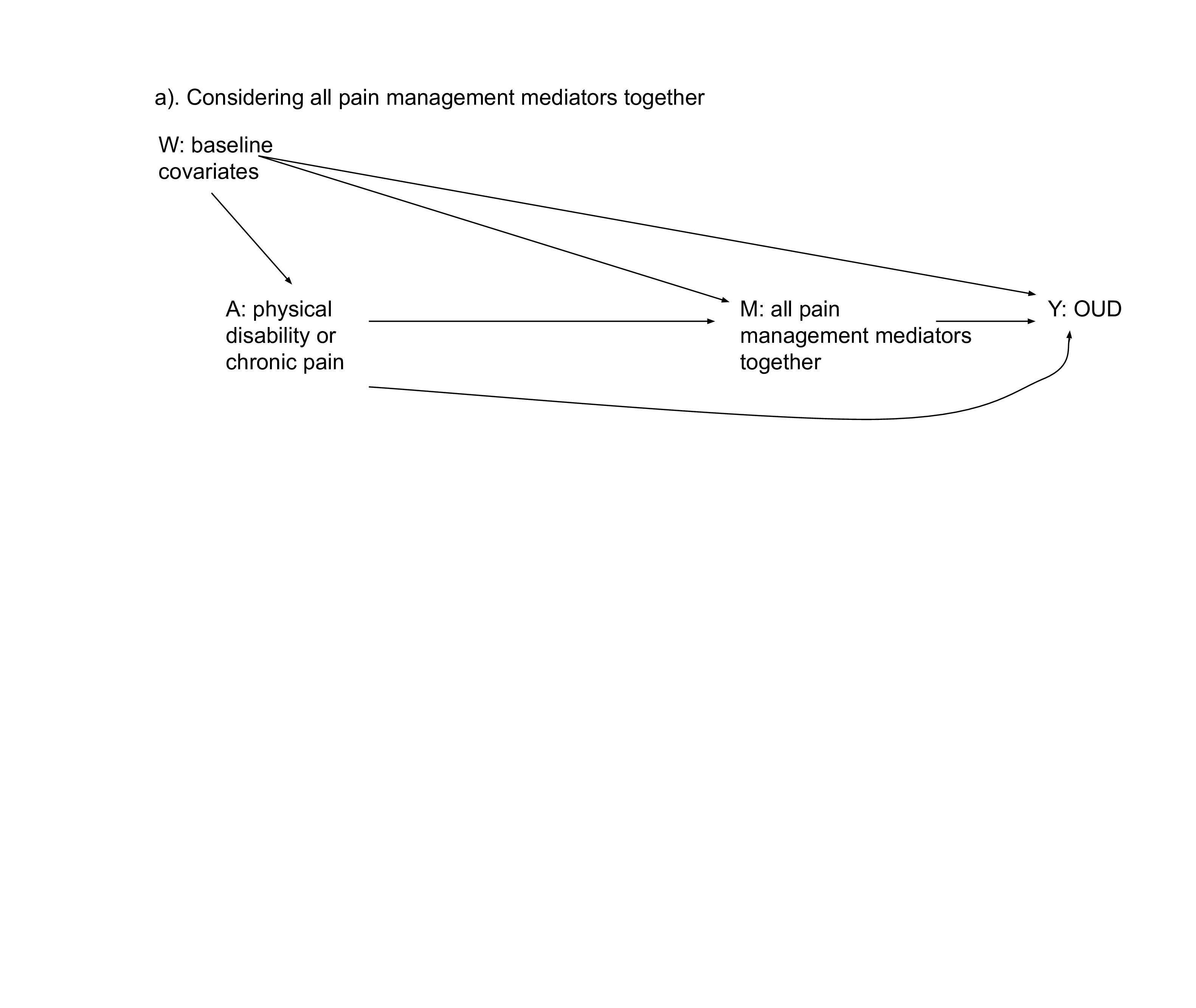
This application was explored in detail by Rudolph et al. (2025)

3.1.1 Getting specific about the question

To what extent does the total effect of chronic pain on risk of OUD operate through prescription medications for pain management and physical therapy, treated as a bundle?

1. What estimand do we want?

• Does \(M=m\) (i.e., same value) for everyone make sense?
• Are we interested in estimating indirect effects?

\(\rightarrow\) So, not a controlled direct effect.

• Do we have an intermediate confounder?
  • Not really, because we: (1) consider all initial treatments following chronic pain diagnosis and (2) stratify by whether the patient has an anxiety or depressive disorder.

\(\rightarrow\) So, could estimate natural direct and indirect effects

• Estimands:
  • Direct effect: \(\E(Y_{1, M_0} - Y_{0, M_0})\)
  • Indirect effect: \(\E(Y_{1, M_1} - Y_{1, M_0})\)

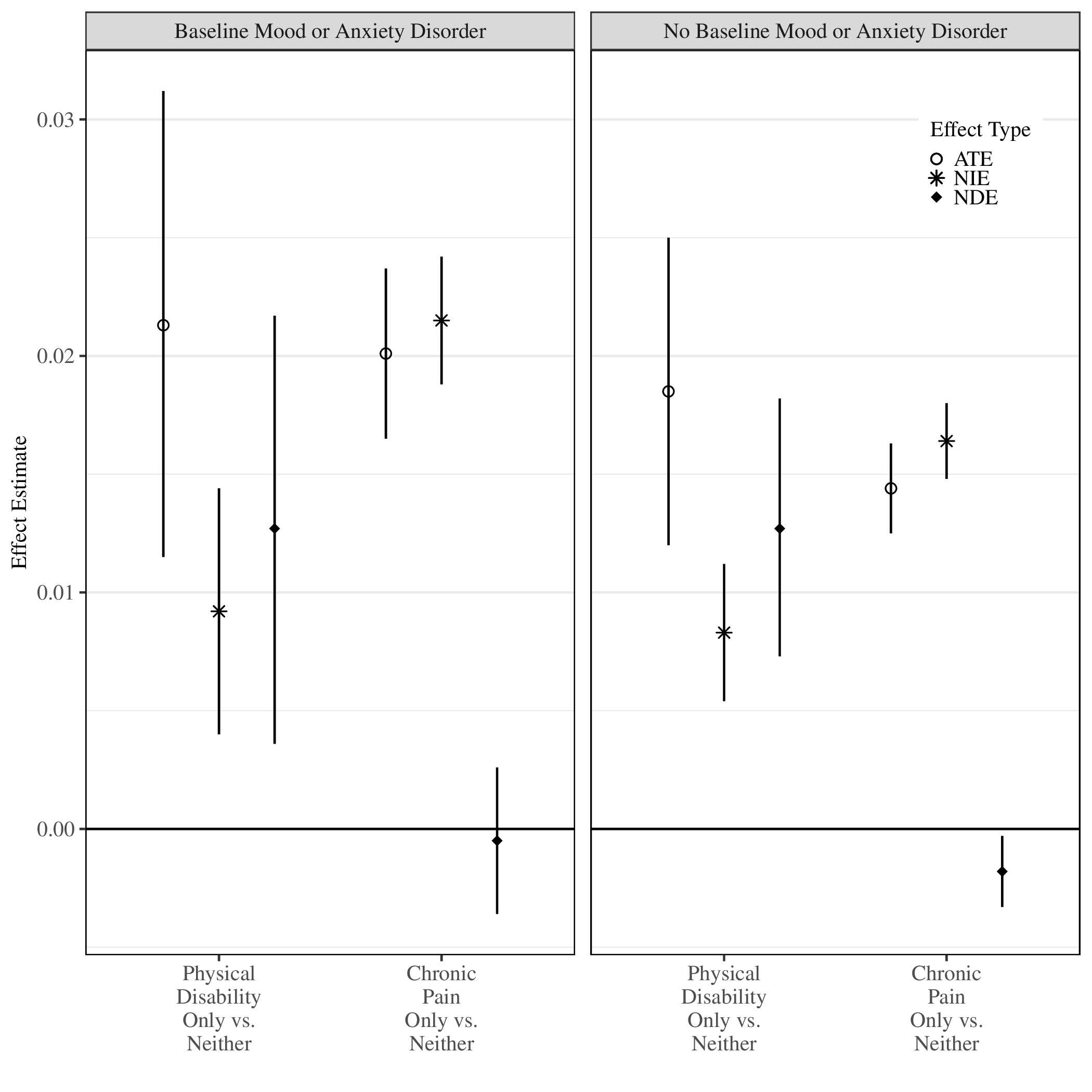
3.2 2. Extent to which the risk of OUD conferred by chronic pain operates through individual pain management treatments

This application was explored in detail and described in Rudolph et al. (2025).

Rudolph, Kara E, Shodai Inose, Nicholas T Williams, Katherine L Hoffman, Sarah E Forrest, Rachael K Ross, Floriana Milazzo, et al. 2025. “Mediation of Chronic Pain and Disability on Opioid Use Disorder Risk by Pain Management Practices Among Adult Medicaid Patients, 2016-2019.” American Journal of Epidemiology, kwaf093.

3.2.1 Getting specific about the question

To what extent does the overall effect of chronic pain on risk of OUD operate through individual pain management treatments, controlling for co-occurring or prior pain treatments?

1. What estimand do we want?

• Does \(M=m\) (i.e., same value) for everyone make sense?
• Are we interested in estimating indirect effects?

\(\rightarrow\) So, not controlled direct effect.

• Do we have an intermediate confounder?
  • Yes, likely multiple important ones, because we would like to control for prior or co-occurring pain treatments.
  • So likely do not have a single, binary intermediate confounder.
  • If we do have a binary intermediate confounder, would we assume monotonicity between the treatment and intermediate confounder?
    • No

\(\rightarrow\) Randomized interventional direct and indirect effects.

• Do we want to estimate the path through treatment initiation (\(Z\))?
  • Yes, so, not the conditional versions of these effects.
  • Here \(G_a\) is a draw from the distribution of \(M_a\mid W\).
• Estimands:
  • Direct effect: \(\E(Y_{1,G_0} - Y_{0,G_0})\)
  • Indirect effect: \(\E(Y_{1,G_1} - Y_{1,G_0})\)
• Need to incorporate multiple and continuous intermediate confounders

2. What if the positivity assumption \(\P(A=a\mid W)>0\) violated?

   \(\rightarrow\) Can’t identify or estimate any of the above effects

   • But we can estimate the effect of some stochastic interventions, e.g., incremental propensity score interventions (IPSIs) (Kennedy 2018)
   • Trade-off between feasibility and interpretation

3. What if the exposure variable is continuous?

   \(\rightarrow\) All the above effects are defined for binary exposures

   • But we can estimate the effect of some stochastic interventions and general interventions on continuous exposures, like shift interventions (also called modified treatment policies) (Dı́az and van der Laan 2012, 2018; Haneuse and Rotnitzky 2013; Dı́az and Hejazi 2020)

4. What if the exposure is actually time-varying? What if the mediators and/or intermediate confounders are actually time-varying?

   • this is hard! but we have two estimation strategies for this:
     • https://github.com/nt-williams/lcmmtp
     • https://github.com/nt-williams/lcm

Kennedy, Edward H. 2018. “Nonparametric Causal Effects Based on Incremental Propensity Score Interventions.” Journal of the American Statistical Association, no. just-accepted.

Dı́az, Iván, and Mark J van der Laan. 2012. “Population Intervention Causal Effects Based on Stochastic Interventions.” Biometrics 68 (2): 541–49.

———. 2018. “Stochastic Treatment Regimes.” In Targeted Learning in Data Science: Causal Inference for Complex Longitudinal Studies, 167–80. Springer Science & Business Media.

Haneuse, Sebastian, and Andrea Rotnitzky. 2013. “Estimation of the Effect of Interventions That Modify the Received Treatment.” Statistics in Medicine 32 (30): 5260–77.

Dı́az, Iván, and Nima S Hejazi. 2020. “Causal Mediation Analysis for Stochastic Interventions.” Journal of the Royal Statistical Society: Series B (Statistical Methodology) 82 (3): 661–83.